tqec.templates#
Defines several scalable arrays of numbers used to tile plaquettes.
This module defines the Template interface that
should be implemented by subclasses implementing different templates.
Terminology used#
The template terminology is used to describe an object (instance of a subclass
of the Template class) that can be
“instantiated” into an array of integers from an input integer scaling parameter
\(k\).
A subtemplate is a constant-size sub-array of a template instantiation. For the moment, a subtemplate is always a square sub-array with odd-sized sides.
The scaling parameter \(k\) directly relates to the code distance \(d\) (at least for regular surface code) where \(d = 2 k + 1\).
Templates#
As noted in the terminology section, a “template” is defined as something that can be “instantiated”, i.e., that can generate an array of integer from a given scaling parameter \(k\).
Templates should all inherit from the base Template
class that defines a few abstract methods that have to be overridden by child
classes. The most canonical example of a template is implemented by the
QubitTemplate class: it represents the
arrangement of plaquettes needed to make a logical qubit.
The following code demonstrates quite well what a template is supposed to be.
from tqec.templates.display import display_template
from tqec.templates.qubit import QubitTemplate
template = QubitTemplate()
display_template(template, 2)
It outputs
1 5 6 5 6 2
7 9 10 9 10 11
8 10 9 10 9 12
7 9 10 9 10 11
8 10 9 10 9 12
3 13 14 13 14 4
The template instantiation is an array of size \(6 \times 6\), filled with
integers. Each unique integer will eventually either be linked to a plaquette or
be left empty. Let’s try to clean up a little bit the array by setting the
values 1, 2, 3, 4, 5, 8, 12 and 14 to the value
0 that means “no plaquette here” for all templates (and that is represented
by . for visibility).
k = 2
removed_plaquettes = {1, 2, 3, 4, 5, 8, 12, 14}
display_template(
template, k, [i if i not in removed_plaquettes else 0 for i in range(1, 15)]
)
that outputs
. . 6 . 6 .
7 9 10 9 10 11
. 10 9 10 9 .
7 9 10 9 10 11
. 10 9 10 9 .
. 13 . 13 . .
The above array looks very much like a logical qubit arrangement as can be seen in most of the papers using the surface code and below!
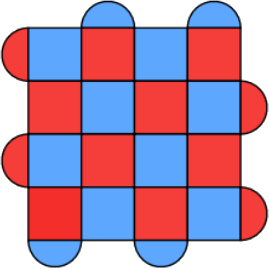
But that is only a distance \(5 = 2 \times 2 + 1 = 2 k + 1\) code. Let’s try to scale that up:
k = 5
display_template(
template, k, [i if i not in removed_plaquettes else 0 for i in range(1, 15)]
)
outputs what we would expect: the “template” of plaquettes for a logical qubit using a distance \(d = 2 k + 1 = 2 \times 5 + 1 = 11\) code:
. . 6 . 6 . 6 . 6 . 6 .
7 9 10 9 10 9 10 9 10 9 10 11
. 10 9 10 9 10 9 10 9 10 9 .
7 9 10 9 10 9 10 9 10 9 10 11
. 10 9 10 9 10 9 10 9 10 9 .
7 9 10 9 10 9 10 9 10 9 10 11
. 10 9 10 9 10 9 10 9 10 9 .
7 9 10 9 10 9 10 9 10 9 10 11
. 10 9 10 9 10 9 10 9 10 9 .
7 9 10 9 10 9 10 9 10 9 10 11
. 10 9 10 9 10 9 10 9 10 9 .
. 13 . 13 . 13 . 13 . 13 . .
This ability to scale to arbitrarily large values of \(k\) (as long as your
computer can store a matrix of shape \((2k+1, 2k+1)\)) is exactly the reason
of existence of the Template class.
This module also includes a few sub-classes implementing the
Template interface:
QubitTemplatethat has already been used in documentation and that represents a logical qubit.QubitSpatialCubeTemplatethat represents a a logical qubit with all the spatial boundaries in the same basis.LayoutTemplatethat represent an arbitrary layout of other templates arranged on a regular grid.
Sub-templates#
This module also implements helpers to list and represent sub-templates. A sub-template is basically a sub-array of a given template instantiation. Sub-templates are all of known constant size and cannot be scaled. Sub-templates are represented as an array of integers with a square shape (i.e., 2-dimensional with the same number of elements in each dimension) with odd-sized sides.
The module tqec.templates.subtemplates provides functions to compute
all the subtemplates for given template instantiation and subtemplate size along
with some data-structure to represent efficiently this collection of
sub-templates.
Displaying#
Templates are basically scalable arrays of integers. The module
tqec.templates.display provides a few functions to display a pretty and
human readable representation of a given template instantiation. These functions
are used in the documentation about templates above, and so their output can be
observed above.